O que é a distribuição normal?

A distribuição normal é uma distribuição contínua de probabilidade associada a uma variável aleatória X. Seu gráfico é conhecido como curva normal e apresenta diversas propriedades fundamentais que a tornam central na estatística e nas finanças quantitativas:

1. Média, mediana e moda são iguais, refletindo uma distribuição perfeitamente simétrica;
2. O formato da curva lembra um sino, simétrico em torno da média;
3. A área total sob a curva é igual a 1, o que representa 100% das probabilidades possíveis;
4. A curva se aproxima do eixo x à medida que se afasta da média, mas nunca o toca.
5. distribuições normais são simétricas, mas nem todas as distribuições simétricas são normais.

O modelo de distribuição normal é fundamental para o Teorema do Limite Central (LTC), que afirma que médias calculadas a partir de variáveis aleatórias independentes e distribuídas de forma idêntica têm distribuições aproximadamente normais, independentemente do tipo de distribuição da qual as variáveis são amostradas.

Parâmetros que definem a curva normal

Dois parâmetros estatísticos completamente determinam o formato da curva:

• µ (média): indica o centro ou eixo de simetria da distribuição; muitas vezes refere-se ao retorno médio esperado de um determinado ativo ou carteira de ativos;
• σ (desvio padrão): expressa a dispersão dos dados em torno da média.

Quanto maior o desvio padrão, mais achatada e espalhada será a curva. Por outro lado, um desvio padrão pequeno gera uma curva mais estreita e alta, com dados mais concentrados em torno da média.

A distribuição normal padronizada

Ao definir μ=0 e σ=1, obtemos a chamada distribuição normal reduzida ou padronizada, representada pela variável aleatória Z. Essa padronização permite comparar diferentes distribuições e calcular probabilidades de forma prática usando a tabela da distribuição normal padrão.

A fórmula para transformar qualquer valor X de uma distribuição normal qualquer em Z é:

Z = (X – μ) / σ

Essa transformação converte qualquer curva normal em uma curva padronizada, permitindo o uso direto da tabela Z.

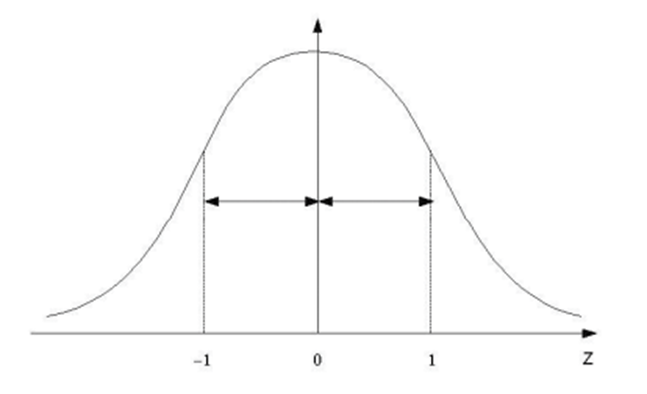
Intervalos de confiança mais utilizados

Na prática, os seguintes intervalos são amplamente aplicados em finanças e estatística inferencial:

• 68% das observações estão entre μ ± 1σ
• 90% das observações estão entre μ ± 1,65σ
• 95% das observações estão entre μ ± 1.96σ
• 99% das observações estão entre μ ± 2,58σ

Esses valores são essenciais para avaliações de risco, análises de desempenho e construção de intervalos de confiança para projeções financeiras.

Aplicações no mercado financeiro

A distribuição normal é utilizada em diversos modelos financeiros, como:

• Value at Risk (VaR): estima perdas potenciais com base na distribuição dos retornos;
• Índice de Sharpe e Treynor: avaliam desempenho ajustado ao risco com base na variância dos retornos;
• Modelos de precificação de opções, como o Black-Scholes, que assumem retornos normalmente distribuídos.

Contudo, é importante observar que, apesar de seu uso disseminado, a distribuição normal subestima eventos extremos, conhecidos como “caudas gordas”. Por isso, muitos analistas complementam suas análises com distribuições alternativas.

Exemplo prático de distribuição normal no mercado financeiro

Situação:

Calcule a probabilidade de P (50 ≤ X ≤ 56), sabendo que a variável aleatória X segue uma distribuição normal com:

• Média (µ) = 50
• Variância = 25, portanto, o desvio padrão (σ) = √25 = 5

Passo 1: Transformar os limites em valores de Z

Utilizamos a fórmula de padronização:

Z = (X – μ) / σ

Para X = 50:

Z = (50 – 50) / 5 = 0

Para X = 56:

Z = (56 – 50) / 5 = 6 / 5 = 1,2

Passo 2: Buscar as probabilidades na tabela Z

• P (Z ≤ 0) = 0,5000
• P (Z ≤ 1,2) ≈ 0,8849

Passo 3: Calcular a probabilidade entre os dois valores

P (50 ≤ X ≤ 56) = P(Z ≤ 1,2) − P(Z ≤ 0)
P (50 ≤ X ≤ 56) = 0,8849 − 0,5000
P (50 ≤ X ≤ 56) = 0,3849

Conclusão:

A probabilidade de a variável X estar entre 50 e 56 é de 38,49%.

Esse tipo de cálculo é essencial para:

• Análise de performance de ativos;
• Estimativas de intervalo de retorno;
• Avaliação de risco em distribuições simétricas.

Dominar a distribuição normal é essencial para qualquer profissional do mercado financeiro. Ela oferece uma base sólida para avaliação de riscos, construção de portfólios e tomada de decisão baseada em estatística. Na Capriata Cursos, você aprende a aplicar esse conceito com profundidade e visão crítica — sabendo exatamente quando usá-lo e quando superá-lo.